チョムスキー標準形のSCFG

非終端記号\(W_1,\ldots,W_M\)の添え字を\(v,y,z\)とする. 開始非終端記号は\(W_1\).
確率付き生成規則の形は以下のいずれかの形
遷移確率　\(t_v(y,z)\)：　\(W_v \rightarrow W_yW_z\)
出力確率　\(e_v(a)\)：　\(W_v \rightarrow a\)　
配列\(x_{1\ldots L}=x_1,\ldots,x_L\)の添え字を\(i,j,k\)とする.

内側アルゴリズム

\(x_{i\ldots j}=x_i,\ldots,x_j\)が\(M_v\)で構文解析される確率\(\alpha(i,j,v)\)の動的計画法

初期化： for \(i = 1\) to \(L\), \(v = 1\) to \(M\):
\( \alpha(i,i,v) = e_v(x_i) \)
再帰： for \(\ell=1\) to \(L\), \(i=1\) to \(L-\ell\), (\(j=i+\ell)\),\(v=1\) to \(M\)
\(
\alpha(i,j,v) = \sum_{y,z=1}^M \sum_{k=i}^{j-1}
\alpha(i,k,y)\alpha(k+1,j,z)t_v(y,z)
\)
終了処理：　\(P(x|\theta) = \alpha(1,L,1)\)

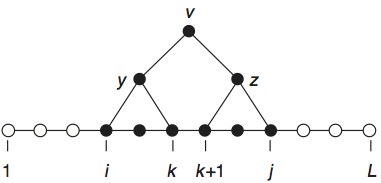
状態\(v\)を根とする構文解析部分木の位置\(i\)から\(j\)までの部分配列に対する内側確率\(\alpha(i,j,v)\)の計算の様子．
\(v \rightarrow yz\)の遷移確率で重みづけし， 状態\(y\)が部分配列\(x_i,\ldots x_k\)， 状態\(z\)が部分配列\(x_{k+1},\ldots x_j\)を
生成するような構文解析部分木を， すべての状態\(y,z\)と部分配列の境目\(k\)について足し込むことにより，
再帰的に計算される．